Application of Groebner BasesProblemSetup of the problem fricas Z==>Integer; Q==>Fraction Z Type: Void
fricas CP==>DistributedMultivariatePolynomial([a, Type: Void
fricas CF==>Fraction CP Type: Void
fricas P==>DistributedMultivariatePolynomial([d, Type: Void
fricas PX==>UnivariatePolynomial('x,
Type: Void
fricas p(x:PX):PX == x*(1-x) Type: Void
fricas q(y:PX):PX == a*y^2+b*y+c Type: Void
fricas y:PX := m*x+n
Type: UnivariatePolynomial(x,
fricas r:PX := p(x) - d*q(y) fricas Compiling function p with type UnivariatePolynomial(x, fricas Compiling function q with type UnivariatePolynomial(x,
Type: UnivariatePolynomial(x, Compute the solutionWe must first extract the coefficients, since each coefficient of any power of x must vanish if the polynomial r is identically 0. fricas coeffs := coefficients r
Type: List(DistributedMultivariatePolynomial?([d, Now we compute a Groebner basis and then solve for the respective variables. fricas gb := groebner coeffs
Type: List(DistributedMultivariatePolynomial?([d,
fricas egb: List Equation Fraction Polynomial Z := [p=0 for p in gb]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas solve(egb,
Type: List(List(Equation(Fraction(Polynomial(Integer))))) In fact, solve is powerful enough so that it is unnecessary to call the Buchberger algorithm explicitly. fricas ecoeffs: List Equation Fraction Polynomial Z := [p=0 for p in coeffs]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas solve(ecoeffs,
Type: List(List(Equation(Fraction(Polynomial(Integer))))) Of course, the result depends on the order of the variables given to the solve command. ((Unfortunately, the axiom-wiki does not properly show the result, so we have added a semicolon to suppress the output.)) fricas solve(ecoeffs, Type: List(List(Equation(Fraction(Polynomial(Integer)))))
=============================================================== Example code --rrogers, Tue, 02 Dec 2014 23:49:41 +0000 reply fricas ---- Ordered variable lists. Poly_to_Gauss:=[d,
fricas Gauss_to_Poly:=[x,
Type: List(UnivariatePolynomial(x,
fricas ----coefficient arrays. corg := d* matrix [[c,
Type: Matrix(Polynomial(Integer))
fricas ---- Explicit target cgauss := matrix [[0,
Type: Matrix(Integer)
fricas ---- Generalized target ctar := matrix [[w,
Type: Matrix(Polynomial(Integer))
fricas ---- polynomial basis arrays. xorg := matrix ([[1,
Type: Matrix(Polynomial(Integer))
fricas xgauss := matrix([[1,
Type: Matrix(UnivariatePolynomial(x,
fricas ---- Example row(corg * transpose(xorg),
Type: Vector(Polynomial(Integer))
fricas ---- Translation matrix Pascal Pa(n) for 3x3 case ---- see Aceto below for references. Pa(n) == matrix [[1, Type: Void
fricas ---- Scalar matrix Sc(m) == diagonalMatrix [1, Type: Void
fricas ---- Now define transform in matrix form D := corg -(cgauss * Pa(n) * Sc(m)) fricas Compiling function Pa with type Variable(n) -> Matrix(Polynomial(
Integer))fricas Compiling function Sc with type Variable(m) -> Matrix(Polynomial(
Integer))
Type: Matrix(Polynomial(Integer))
fricas ---- Now we do a more realistic solve in two steps ---- Step one disallow silly answers E:=groebnerFactorize(row(D,
Type: List(List(Polynomial(Integer)))
fricas ---- and clean it up (a lot). I wish these two steps could be one! solve(E.1,
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas ---- Now lets test the reasonableness the width to start with is ---- 2*sqrt(b^2-4*a*c)/(2*a) which the left hand term yields. There is a sign ambiguity ---- corresponding to whether the source quadratic is to the left or right. ---- I could swap n,
Type: Matrix(Polynomial(Integer))
fricas Z==>Integer; Q==>Fraction Z Type: Void
fricas CP==>DistributedMultivariatePolynomial([a, Type: Void
fricas CF==>Fraction CP Type: Void
fricas P==>DistributedMultivariatePolynomial([d, Type: Void
fricas PX==>UnivariatePolynomial('x,
Type: Void
fricas p(x:PX):PX == x*(1-x) Type: Void
fricas fp(x:PX):PX == u*x^2+v*x+w Type: Void
fricas q(y:PX):PX == a*y^2+b*y+c; Type: Void
fricas y:PX := m*x+n
Type: UnivariatePolynomial(x,
fricas r:PX := p(x) - d*q(y) fricas Compiling function p with type UnivariatePolynomial(x, fricas Compiling function q with type UnivariatePolynomial(x,
Type: UnivariatePolynomial(x,
fricas s:PX := fp(x) - d*q(y) fricas Compiling function fp with type UnivariatePolynomial(x,
Type: UnivariatePolynomial(x,
fricas coeffs := coefficients r
Type: List(DistributedMultivariatePolynomial?([d,
fricas fcoeffs := coefficients s
Type: List(DistributedMultivariatePolynomial?([d,
fricas gb := groebner coeffs
Type: List(DistributedMultivariatePolynomial?([d,
fricas fgb := groebner fcoeffs
Type: List(DistributedMultivariatePolynomial?([d,
fricas egb: List Equation Fraction Polynomial Z := [p=0 for p in gb]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas fegb: List Equation Fraction Polynomial Z := [p=0 for p in fgb]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas ecoeffs: List Equation Fraction Polynomial Z := [p=0 for p in coeffs]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas fecoeffs: List Equation Fraction Polynomial Z := [p=0 for p in fcoeffs]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas cc:=solve(egb, Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas cc.1
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas dd:=solve(ecoeffs, Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas dd.1
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas fcc:=solve(fegb, Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas fcc.1
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas fdd:=solve(fecoeffs, Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas fdd.1
Type: List(Equation(Fraction(Polynomial(Integer))))
|
|
|
|
last edited 8 years ago by rrogers |
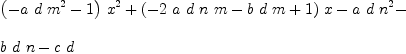
![\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{-{a \ d \ {{m}^{2}}}- 1}, \:{-{2 \ a \ d \ n \ m}-{b \ d \ m}+ 1}, \: \right.
\
\
\displaystyle
\left.{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}\right]
\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{-{a \ d \ {{m}^{2}}}- 1}, \:{-{2 \ a \ d \ n \ m}-{b \ d \ m}+ 1}, \: \right.
\
\
\displaystyle
\left.{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}\right]](/images/8245104986464204879-16.0px.png)
![\label{eq5}\begin{array}{@{}l}
\displaystyle
\left[{{{{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ d}- a}\over{{4 \ a \ c}-{{b}^{2}}}}= 0}, \:{{{{2 \ a \ n}+{a \ m}+ b}\over{2 \ a}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{{{a}^{2}}\ {{m}^{2}}}+{4 \ a \ c}-{{b}^{2}}}\over{{a}^{2}}}= 0}\right]
\label{eq5}\begin{array}{@{}l}
\displaystyle
\left[{{{{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ d}- a}\over{{4 \ a \ c}-{{b}^{2}}}}= 0}, \:{{{{2 \ a \ n}+{a \ m}+ b}\over{2 \ a}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{{{a}^{2}}\ {{m}^{2}}}+{4 \ a \ c}-{{b}^{2}}}\over{{a}^{2}}}= 0}\right]](/images/7841115730631015885-16.0px.png)
![\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{-{a \ d \ {{m}^{2}}}- 1}= 0}, \:{{-{2 \ a \ d \ m \ n}-{b \ d \ m}+ 1}= 0}, \: \right.
\
\
\displaystyle
\left.{{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}= 0}\right]
\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{-{a \ d \ {{m}^{2}}}- 1}= 0}, \:{{-{2 \ a \ d \ m \ n}-{b \ d \ m}+ 1}= 0}, \: \right.
\
\
\displaystyle
\left.{{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}= 0}\right]](/images/4028224099335330876-16.0px.png)
![\label{eq18}\begin{array}{@{}l}
\displaystyle
\left[{
\begin{array}{@{}l}
\displaystyle
\left[{{{n}^{2}}- n +{c \ d}}, \:{{2 \ m \ n}- m +{b \ d}}, \: \right.
\
\
\displaystyle
\left.{{2 \ b \ d \ n}+{{\left(-{4 \ c \ d}+ 1 \right)}\ m}-{b \ d}}, \:{{2 \ a \ n}-{b \ m}- a}, \:{{{m}^{2}}+{a \ d}}, \: \right.
\
\
\displaystyle
\left.{{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ d}- a}\right]
\label{eq18}\begin{array}{@{}l}
\displaystyle
\left[{
\begin{array}{@{}l}
\displaystyle
\left[{{{n}^{2}}- n +{c \ d}}, \:{{2 \ m \ n}- m +{b \ d}}, \: \right.
\
\
\displaystyle
\left.{{2 \ b \ d \ n}+{{\left(-{4 \ c \ d}+ 1 \right)}\ m}-{b \ d}}, \:{{2 \ a \ n}-{b \ m}- a}, \:{{{m}^{2}}+{a \ d}}, \: \right.
\
\
\displaystyle
\left.{{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ d}- a}\right]](/images/7678919746467925014-16.0px.png)
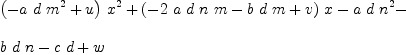
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{-{a \ d \ {{m}^{2}}}- 1}, \:{-{2 \ a \ d \ n \ m}-{b \ d \ m}+ 1}, \: \right.
\
\
\displaystyle
\left.{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}\right]
\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{-{a \ d \ {{m}^{2}}}- 1}, \:{-{2 \ a \ d \ n \ m}-{b \ d \ m}+ 1}, \: \right.
\
\
\displaystyle
\left.{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}\right]](/images/1688423701865309020-16.0px.png)
![\label{eq5}\begin{array}{@{}l}
\displaystyle
\left[{-{a \ d \ {{m}^{2}}}+ u}, \:{-{2 \ a \ d \ n \ m}-{b \ d \ m}+ v}, \: \right.
\
\
\displaystyle
\left.{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}+ w}\right]
\label{eq5}\begin{array}{@{}l}
\displaystyle
\left[{-{a \ d \ {{m}^{2}}}+ u}, \:{-{2 \ a \ d \ n \ m}-{b \ d \ m}+ v}, \: \right.
\
\
\displaystyle
\left.{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}+ w}\right]](/images/8698227003878611606-16.0px.png)
![\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{d +{{-{4 \ a \ u \ w}+{a \ {{v}^{2}}}}\over{{4 \ a \ c \ u}-{{{b}^{2}}\ u}}}}, \:{n -{{v \over{2 \ u}}\ m}+{b \over{2 \ a}}}, \: \right.
\
\
\displaystyle
\left.{{{m}^{2}}+{{-{4 \ a \ c \ {{u}^{2}}}+{{{b}^{2}}\ {{u}^{2}}}}\over{{4 \ {{a}^{2}}\ u \ w}-{{{a}^{2}}\ {{v}^{2}}}}}}\right]
\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{d +{{-{4 \ a \ u \ w}+{a \ {{v}^{2}}}}\over{{4 \ a \ c \ u}-{{{b}^{2}}\ u}}}}, \:{n -{{v \over{2 \ u}}\ m}+{b \over{2 \ a}}}, \: \right.
\
\
\displaystyle
\left.{{{m}^{2}}+{{-{4 \ a \ c \ {{u}^{2}}}+{{{b}^{2}}\ {{u}^{2}}}}\over{{4 \ {{a}^{2}}\ u \ w}-{{{a}^{2}}\ {{v}^{2}}}}}}\right]](/images/4024649792941612684-16.0px.png)
![\label{eq8}\begin{array}{@{}l}
\displaystyle
\left[{{{{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ d}- a}\over{{4 \ a \ c}-{{b}^{2}}}}= 0}, \:{{{{2 \ a \ n}+{a \ m}+ b}\over{2 \ a}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{{{a}^{2}}\ {{m}^{2}}}+{4 \ a \ c}-{{b}^{2}}}\over{{a}^{2}}}= 0}\right]
\label{eq8}\begin{array}{@{}l}
\displaystyle
\left[{{{{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ d}- a}\over{{4 \ a \ c}-{{b}^{2}}}}= 0}, \:{{{{2 \ a \ n}+{a \ m}+ b}\over{2 \ a}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{{{a}^{2}}\ {{m}^{2}}}+{4 \ a \ c}-{{b}^{2}}}\over{{a}^{2}}}= 0}\right]](/images/1057033562557099208-16.0px.png)
![\label{eq9}\begin{array}{@{}l}
\displaystyle
\left[{{{-{4 \ a \ u \ w}+{a \ {{v}^{2}}}+{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ d \ u}}\over{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ u}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{-{a \ m \ v}+{{\left({2 \ a \ n}+ b \right)}\ u}}\over{2 \ a \ u}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{4 \ {{a}^{2}}\ {{m}^{2}}\ u \ w}-{{{a}^{2}}\ {{m}^{2}}\ {{v}^{2}}}+{{\left(-{4 \ a \ c}+{{b}^{2}}\right)}\ {{u}^{2}}}}\over{{4 \ {{a}^{2}}\ u \ w}-{{{a}^{2}}\ {{v}^{2}}}}}= 0}\right]
\label{eq9}\begin{array}{@{}l}
\displaystyle
\left[{{{-{4 \ a \ u \ w}+{a \ {{v}^{2}}}+{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ d \ u}}\over{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ u}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{-{a \ m \ v}+{{\left({2 \ a \ n}+ b \right)}\ u}}\over{2 \ a \ u}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{4 \ {{a}^{2}}\ {{m}^{2}}\ u \ w}-{{{a}^{2}}\ {{m}^{2}}\ {{v}^{2}}}+{{\left(-{4 \ a \ c}+{{b}^{2}}\right)}\ {{u}^{2}}}}\over{{4 \ {{a}^{2}}\ u \ w}-{{{a}^{2}}\ {{v}^{2}}}}}= 0}\right]](/images/1112376277526924279-16.0px.png)
![\label{eq10}\begin{array}{@{}l}
\displaystyle
\left[{{-{a \ d \ {{m}^{2}}}- 1}= 0}, \:{{-{2 \ a \ d \ m \ n}-{b \ d \ m}+ 1}= 0}, \: \right.
\
\
\displaystyle
\left.{{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}= 0}\right]
\label{eq10}\begin{array}{@{}l}
\displaystyle
\left[{{-{a \ d \ {{m}^{2}}}- 1}= 0}, \:{{-{2 \ a \ d \ m \ n}-{b \ d \ m}+ 1}= 0}, \: \right.
\
\
\displaystyle
\left.{{-{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}= 0}\right]](/images/3475673540610227677-16.0px.png)
![\label{eq11}\begin{array}{@{}l}
\displaystyle
\left[{{u -{a \ d \ {{m}^{2}}}}= 0}, \:{{v -{2 \ a \ d \ m \ n}-{b \ d \ m}}= 0}, \: \right.
\
\
\displaystyle
\left.{{w -{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}= 0}\right]
\label{eq11}\begin{array}{@{}l}
\displaystyle
\left[{{u -{a \ d \ {{m}^{2}}}}= 0}, \:{{v -{2 \ a \ d \ m \ n}-{b \ d \ m}}= 0}, \: \right.
\
\
\displaystyle
\left.{{w -{a \ d \ {{n}^{2}}}-{b \ d \ n}-{c \ d}}= 0}\right]](/images/1667856006545328170-16.0px.png)
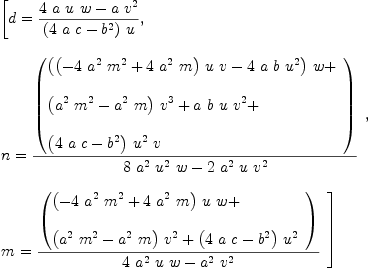
![\label{eq15}\begin{array}{@{}l}
\displaystyle
\left[{d ={{{4 \ a \ u \ w}-{a \ {{v}^{2}}}}\over{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ u}}}, \:{n ={{{a \ m \ v}-{b \ u}}\over{2 \ a \ u}}}, \: \right.
\
\
\displaystyle
\left.{{{4 \ {{a}^{2}}\ {{m}^{2}}\ u \ w}-{{{a}^{2}}\ {{m}^{2}}\ {{v}^{2}}}+{{\left(-{4 \ a \ c}+{{b}^{2}}\right)}\ {{u}^{2}}}}= 0}\right]
\label{eq15}\begin{array}{@{}l}
\displaystyle
\left[{d ={{{4 \ a \ u \ w}-{a \ {{v}^{2}}}}\over{{\left({4 \ a \ c}-{{b}^{2}}\right)}\ u}}}, \:{n ={{{a \ m \ v}-{b \ u}}\over{2 \ a \ u}}}, \: \right.
\
\
\displaystyle
\left.{{{4 \ {{a}^{2}}\ {{m}^{2}}\ u \ w}-{{{a}^{2}}\ {{m}^{2}}\ {{v}^{2}}}+{{\left(-{4 \ a \ c}+{{b}^{2}}\right)}\ {{u}^{2}}}}= 0}\right]](/images/3216506723505631168-16.0px.png)