Biquaternion Calculus Domain

D. Cyganski and Bill Page - July 2007

This version is implemented as a new domain in Aldor .

(1) -> <aldor>
#pile
#include "axiom"

import from NonNegativeInteger

BiQuaternion(R:Join(OrderedSet,CommutativeRing)): Exports == Implementation where
  C==>Complex Expression R
  Exports ==> QuaternionCategory(C) with
    qlist: List C -> %
    -- takes a complex list (parameter l) into a quaternion
    listq: % -> List C
    -- takes a quaternion into a list
    matrixq: % -> SquareMatrix(2,C)
    -- takes a quaternion into a matrix
    sig0:%
    sig1:%
    sig2:%
    sig3:%
    siglist: % -> List C
    -- Pauli basis representation of the biquaternion
    if Complex(Expression(R)) has PartialDifferentialRing(Symbol) then
      D: (%,Symbol,Symbol,Symbol) -> %
    -- quaternion derivative
    rot: (C,%) -> %
    -- biquaternion rotation
    /: (%,%) -> %
    /: (C,%) -> %
    /: (%,C) -> %
    abs: % -> C
    exp: % -> %
    coerce: Complex R -> %

  Implementation ==> Quaternion C add
    import from C

    coerce(z:Complex R):% ==
      import from Expression(R),ComplexFunctions2(R,Expression R)
      map(coerce,z)::%

    -- Define a function that takes a complex list (parameter l) into a quaternion
    qlist(l:List C):%==
      import from Integer
      quatern(l 1,l 2,l 3,l 4)
    -- Define a function that takes a quaternion into a list
    listq(x:%):List C == [real x, imagI x, imagJ x, imagK x]
    -- Define a function that takes a biquat into a matrix
    matrixq(x:%):SquareMatrix(2,C) ==
       import from List List C
       matrix [[real x + imaginary()*imagI(x), imagJ x + imaginary()*imagK(x)],
               [-imagJ(x) + imaginary()*imagK(x), real x - imaginary()*imagI(x)]]
    -- Define a function that produces the Pauli basis representation of the biquaternion
    siglist(x:%):List C == [real x, -imaginary()*imagK(x),-imaginary()*imagJ(x),imaginary()*imagI(x)]
    sig0:% == quatern(1,0,0,0)
    sig1:% == imaginary() * quatern(0,0,0,1)
    sig2:% == imaginary() * quatern(0,0,1,0)
    sig3:% == -imaginary() * quatern(0,1,0,0)
    -- Define the quaternion derivative (Morgan, 2001, Eq. 2)
    if Complex(Expression(R)) has PartialDifferentialRing(Symbol) then
      D(q:%,x:Symbol,y:Symbol,z:Symbol):% == sig1*D(q,x)+sig2*D(q,y)+sig3*D(q,z)
    -- Define a biquaternion rotation operator that takes a biquat through a rotation
    -- of theta radians about the axis defined by the unit q biquat (Morgan 2001, Eq 3).
    rot(theta:C,q:%):% ==
      import from Integer, SparseMultivariatePolynomial(Integer, Kernel(C))
      cos(theta/2::C)::% - imaginary()*q*sin(theta/2::C)
    ((x:%)/(y:%)):% == x*inv(y)
    ((x:C)/(y:%)):% == (x::%)*inv(y)
    ((x:%)/(y:C)):% == x*inv(y::%)
    abs(q:%):C ==
      sqrt(retract(q*conjugate(q)))
    exp(q:%):% ==
      import from Integer, SparseMultivariatePolynomial(Integer, Kernel(C))
      q-conjugate(q)=0 => exp(retract(q+conjugate(q))/2::C)*sig0
      exp(retract(q+conjugate(q))/2::C) * (sig0*cos(abs(q)) + (q-conjugate(q))/abs(q-conjugate(q)) * sin(abs(q)))</aldor>

Compiling FriCAS source code from file 
      /var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/7484925992146577797-25px001.as
      using Aldor compiler and options 
-O -Fasy -Fao -Flsp -lfricas -Mno-ALDOR_W_WillObsolete -DFriCAS -Y $FRICAS/algebra -I $FRICAS/algebra
      Use the system command )set compiler args to change these 
      options.
   The )library system command was not called after compilation.

)show BiQuaternion

   The )show system command is used to display information about types 
      or partial types. For example, )show Integer will show 
      information about Integer .

      BiQuaternion is not the name of a known type constructor. If you 
      want to see information about any operations named BiQuaternion ,
      issue
                      )display operations BiQuaternion

Q := BiQuaternion Integer

   There are no library operations named BiQuaternion 
      Use HyperDoc Browse or issue
                            )what op BiQuaternion
      to learn if there is any operation containing " BiQuaternion " in
      its name.

   Cannot find a definition or applicable library operation named 
      BiQuaternion with argument type(s) 
                                    Type

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

For testing the derivative we define this set of operators

Ft:=operator 'Ft; Fx:=operator 'Fx; Fy:=operator 'Fy; Fz:=operator 'Fz;

Now form a general quaternion which is a function of x,y,z

F:Q:=Ft(x,y,z)*sig0()+Fx(x,y,z)*sig1()+Fy(x,y,z)*sig2()+Fz(x,y,z)*sig3()

   Q is not a valid type.

In the Pauli basis the derivative of this biquat should produce (Morgan 2001, eq 1):

  D(Ft+F.sigma)=div(F)+(grad(Ft)+%i*curl(F)).sigma

which it does

siglist(D(F,x,y,z))

   There are no library operations named D having 4 argument(s) though 
      there are 11 exposed operation(s) and 4 unexposed operation(s) 
      having a different number of arguments. Use HyperDoc Browse, or 
      issue
                                 )what op D
      to learn what operations contain " D " in their names, or issue
                                )display op D
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named D 
      with argument type(s) 
                                 Variable(F)
                                 Variable(x)
                                 Variable(y)
                                 Variable(z)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Test

(comment out this test later)

%i::Q

   Q is not a valid type.

If I've defined these correctly, then the rotation about the x axis defined by qx below by 2 radians should give the same answer as exponentiation to -%i*qx (not a very complete test)

qx:Q:=sig1()

   Q is not a valid type.

which it does

(%%(-1)=%%(-2))@Boolean

   Cannot supply value for step 0 because 1 is the first step.

I would love to express a proof of equality such as:

   rot(theta,q) = exp((-theta/2)*%i*q)

for arbitrary real 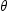and biquaternion q as I would in Maple.

theta:Complex Expression Integer := _\theta

(1)

map(simplify, siglist( rot(theta,q) - exp((-%i*theta/2) * q)))::List Expression Complex Integer

   There are no library operations named rot 
      Use HyperDoc Browse or issue
                                )what op rot
      to learn if there is any operation containing " rot " in its 
      name.

   Cannot find a definition or applicable library operation named rot 
      with argument type(s) 
                        Complex(Expression(Integer))
                                 Variable(q)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

map(simplify,siglist(rot(2,qx)))::List Expression Complex Integer

   There are no library operations named rot 
      Use HyperDoc Browse or issue
                                )what op rot
      to learn if there is any operation containing " rot " in its 
      name.

   Cannot find a definition or applicable library operation named rot 
      with argument type(s) 
                               PositiveInteger
                                Variable(qx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.