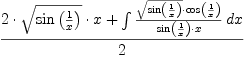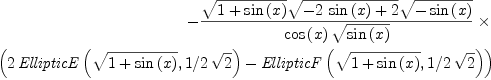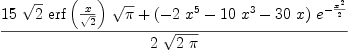MathAction Symbolic Integration

Topics

FrontPage
- FAQ
  - FriCAS Problems
    - Symbolic Integration <-- You are here.

RischImplementationStatus

Errors in symbolic integration

Risch-Bronstein-Trager algorithm (Risch algorithm in short) is a complete algorithom for integration in terms of elementary functions. The algorithm either finds elementary integral or proves that there is none. Existence of elementary integral is relatively rare, so given random elementary function probably does not have elementary integral. FriCAS implementation of Risch algorithm is probably the "most complete" existing implementation. Unfortunatly "most complete" does not mean complete, some parts are still unimplemented. See RischImplementationStatus. Unlike some other systems FriCAS will not give you unevaluated result when hitting unimplemented part. Instead, it signals error with message indicating that given integral requires unimplemented part. So when FriCAS returns unevaluated result almost surely there is on elementary integral. Almost surely, because as all programs FriCAS may have bugs...

FriCAS in fact implements extension of Risch algorithm which extends class of integrands to some Liouvillian functions and for integration in terms of Ei, Ci, Si, li, erf, fresnelS, fresnelC, incomplete Gamma and polylog. There is complete extended algorithm for large class of functions (but polylog causes tricky theoretical problems). Compared to theory current FriCAS implementation contains considerable gaps. Nevertheless, FriCAS can handle a lot of examples involving special functions that no other system can handle.

Additionaly to Risch integrator FriCAS contains relativly weak pattern matching integrator which can generate a few special functions -- Ei, li, dilog and erf. However, if integral really requires elliptic functions then the best thing which FriCAS can do is to prove that integral is nonelementary.

FriCAS Examples

fricas

integrate(sin(x)+sqrt(1-x^3),x)

$\label{eq1}\int^{ \displaystyle x}{{\left({\sqrt{-{{\%A}^{3}}+ 1}}+{\sin \left({\%A}\right)}\right)}\ {d \%A}}$

(1)

Type: Union(Expression(Integer),...)

Unevaluated result means that FriCAS proved that result is not elementary and can not find nonelementary result.

int(sin(x)+sqrt(1-x^3),x);

reduce

$\displaylines{\qdd \frac{-5\cdot \cos \(x$

fricas

integrate(sqrt(1-log(sin(x)^2)),x)

   >> Error detected within library code:
   integrate: implementation incomplete (constant residues)

In this case FriCAS neither can compute elementry result nor can it prove that result is not elementary, is it gives up with error message indicating that the handling this integral requires unimplemented part of Bronstein-Trager algorithm.

int(sqrt(1-log(sin(x)^2)),x);

reduce

$\displaylines{\qdd \int {\sqrt{ -\ln \(\sin \(x$

fricas

integrate(sqrt(sin(1/x)),x)

   >> Error detected within library code:
   integrate: implementation incomplete (constant residues)

Again, this integral needs unimplemented part of Bronstein-Trager algorithm.

int(sqrt(sin(1/x)),x);

reduce

$\displaylines{\qdd \frac{2\cdot \sqrt{\sin \(\frac{1}{ x}$

fricas

integrate(sqrt(sin(x)),x)

$\label{eq2}\int^{ \displaystyle x}{{\sqrt{\sin \left({\%A}\right)}}\ {d \%A}}$

(2)

Type: Union(Expression(Integer),...)

This time FriCAS can prove that result is nonelementary (it needs elliptic functions).

int(sqrt(sin(x)),x);

reduce

$\displaylines{\qdd \int {\sqrt{\sin \(x$

For this Maple 9 gives the following result:

$\label{eq3} -{\frac {\sqrt {1+\sin \left( x \right) }\sqrt {-2\,\sin \left( x \right) +2}\sqrt {-\sin \left( x \right) }}{\cos \left( x \right) \sqrt {\sin \left( x \right) }}} \times \ \left( 2\,{\it EllipticE} \left( \sqrt {1+\sin \left( x \right) },1/2\,\sqrt {2} \right) -{\it EllipticF} \left( \sqrt {1+\sin \left( x \right) },1/2\,\sqrt {2} \right) \right)$

(3)

And Mathematica 4 gives:

$\label{eq4} -2\,{\it EllipticE}(\frac{\frac{\pi }{2} - x}{2},2)$

(4)

symbolic integration: Tue, 22 Mar 2005 11:48:00 -0600 reply

fricas

integrate(exp(-x^2),x)

$\label{eq5}{{\erf \left({x}\right)}\ {\sqrt{\pi}}}\over 2$

(5)

Type: Union(Expression(Integer),...)

Errorfunction

Wed, 23 Mar 2005 08:23:21 -0600 reply

fricas

integrate(exp(-x^2/2)/sqrt(%pi*2),x=%minusInfinity..%plusInfinity)

$\label{eq6}{{\sqrt{2}}\ {\sqrt{\pi}}}\over{\sqrt{2 \ \pi}}$

(6)

Type: Union(f1: OrderedCompletion?(Expression(Integer)),...)

... --unknown, Sat, 21 May 2005 12:52:20 -0500 reply

Works, roots remain unsimplified to preserve branches:

fricas

integrate(x^6*exp(-x^2/2)/sqrt(%pi*2),x=%minusInfinity..%plusInfinity)

$\label{eq7}{{15}\ {\sqrt{2}}\ {\sqrt{\pi}}}\over{\sqrt{2 \ \pi}}$

(7)

Type: Union(f1: OrderedCompletion?(Expression(Integer)),...)

fricas

integrate(x^6*exp(-x^2/2)/sqrt(%pi*2),x)

$\label{eq8}{{{15}\ {\sqrt{2}}\ {\erf \left({x \over{\sqrt{2}}}\right)}\ {\sqrt{\pi}}}+{{\left(-{2 \ {{x}^{5}}}-{{10}\ {{x}^{3}}}-{{30}\ x}\right)}\ {{e}^{-{{{x}^{2}}\over 2}}}}}\over{2 \ {\sqrt{2 \ \pi}}}$